El premio Nobel de Física 2025
La intuición que desarrollamos en la vida cotidiana resulta inútil y contraproducente cuando se trata de comprender el comportamiento del mundo cuántico, el cual descubrimos hace poco más de 100 años. El ámbito macroscópico actual, obedece unas reglas que son, por mucho, muy diferentes de las normas que obedecen partículas tan diminutas como los electrones. La evolución ha privilegiado la detección sensorial de las interacciones que se manifiestan, de alguna forma a nuestra escala, para responder a ellas usando nuestro cuerpo. Así, el mundo cuántico nos ha sido vedado: no se puede ver, oler, sentir, oír o gustar. Tropezamos con él gracias a que hemos conseguido extender la aplicabilidad de los cinco sentidos con aparatos de medición cada vez más sofisticados y precisos.
La Física Cuántica estudia el comportamiento de los elementos fundamentales de aquello que llamamos materia o energía -en la actualidad, gracias a la muy conocida ecuación de Einstein, E=mc2–, entendemos que estos dos conceptos están interconectados: la materia puede transformarse en energía y viceversa. Los átomos, por ejemplo, se componen de un núcleo, formado por neutrones y protones, por lo que estas partículas también son conocidas como nucleones y una nube de electrones que lo circunda. Estas tres partículas, los nucleones y el electrón, evitan aglomerarse y solo admiten agruparse de formas muy específicas que son dictadas por la estadística de Fermi-Dirac (también son llamadas Fermiones). Un fotón es la cantidad mínima de energía que puede obtenerse -o suministrar- a la radiación electromagnética. Los fotones se caracterizan por la frecuencia v de la señal electromagnética. La cantidad de energía que representan está dada por otra ecuación de Einstein, E=hv, donde h es la constante de Planck. En el caso de la luz, v se refiere al color, y no tiene dificultades en aglomerarse siempre que la forma en la que se agrupen obedezca la estadística de Bose-Einstein, por lo que también se les llama Bosones.
Dos de las manifestaciones más inusuales del mundo cuántico son el entrelazamiento cuántico y el efecto túnel. Es notable que hace poco más de noventa años no se tenía idea de la existencia del primero, por lo que su entendimiento y verificación experimental son recientes. Este se refiere a una propiedad sorprendente de los estados cuánticos que trasciende las características locales de los sistemas involucrados. Su impacto en el entendimiento del mundo cuántico, así como en el surgimiento y desarrollo de tecnológicas cuánticas, ha sido reconocido con el Premio Nobel de Física 2022, entregado a Alain Aspect, John. F. Clauser y Anton Zeilinger [1]. El entendimiento del efecto túnel se consiguió a la par de la culminación de la estructura formal de la Mecánica Cuántica, por lo que su importancia fue resaltada desde hace 53 años con el Premio Nobel de Física 1972, entregado a Leo Esaki e Ivar Giaever por los descubrimientos experimentales asociados con el fenómeno del efecto túnel en semiconductores y superconductores, respectivamente, y a Brian David Josephson por la predicción teórica de las propiedades de la supercorriente que surge por el efecto túnel, en particular aquellas asociadas con los fenómenos conocidos como efectos Josephson[2].
Con el fin de precisar el concepto del efecto túnel recordemos algunas nociones básicas de la Física Newtoniana. La energía mecánica total E de una partícula se compone de la suma de la energía cinética T y la energía potencial V, es decir E=T+V. Por definición, la energía cinética es no negativa, por lo que encontramos E≥V. En otras palabras, la energía mecánica total es siempre mayor, (partícula en movimiento, T≠0) o igual (partícula en reposo, T=0), que la energía potencial. Para investigar lo que ocurre cuando esta restricción no se cumple, consideremos una partícula de masa m que se desplaza a lo largo del eje x con velocidad v≥0. Tenemos la energía cinética T=P2/2m’ , donde P=mv es el momento lineal. De la expresión T=E-V obtenemos P2=2m(E-V). Así que las energías E que son inferiores al potencial V implican cantidades P2 negativas (P2<0), por lo que el momento lineal correspondiente sería un P=imv número imaginario puro, . Esto último es inadmisible en la Física Newtoniana ya que su cumplimiento requiere de masas imaginarias puras (im) o de velocidades imaginarias puras (iv).
Las limitaciones impuestas por la combinación de energías cinética y potencial, define regiones clásicamente prohibidas en Mecánica Clásica. Por ejemplo, supongamos que el potencial tiene la forma de una barrera de ancho d y altura V0 (Figura 1). Fuera de la región espacial delimitada por d la energía potencial es igual a cero, por lo que la partícula se mueve libremente con energía cinética T=P2/2m’ . Para energías E>V0, la partícula puede estar incluso en la región d. No obstante, dicha región está prohibida si la partícula tiene energía E<V0. En este caso, la partícula cambiará la dirección de su movimiento tan pronto se tropiece con la barrera de potencial, por lo que estará confinada a moverse exclusivamente en una región concreta de la recta. Por ejemplo, si su movimiento hacia el potencial es de izquierda a derecha, la partícula será “rebotada” a la izquierda y se verá impedida de ocupar la región que se encuentra a la derecha de la barrera.
[caption id="attachment_11798" align="aligncenter" width="591"]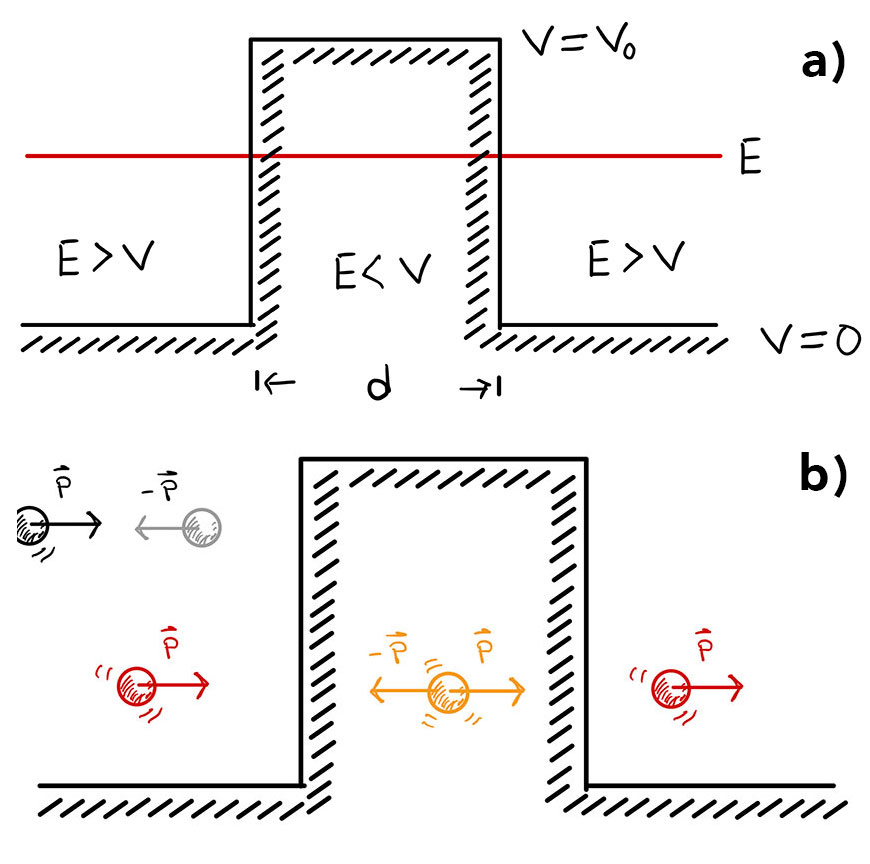
Figura 1. (a) La región d al interior de la barrera de potencial está prohibida clásicamente cuando la energía mecánica total de la partícula es inferior a la altura del potencial (E<V0). Fuera de dicha región la partícula se mueve con momento lineal P=mv. (b) Una partícula clásica que se mueve de izquierda a derecha con momento lineal P cambia la dirección de su movimiento al llegar a la región clásicamente prohibida, por lo que queda confinada a moverse solo a la izquierda de la barrera de potencial (partículas en negro y gris). El confinamiento clásico no aplica si se trata de una partícula cuántica (caricaturizada en rojo y naranja). La partícula puede ocupar la región clásicamente prohibida, incluso atravesándola por completo para continuar su movimiento hacia la derecha, más allá de la barrera de potencial. Esto último se conoce como efecto túnel.[/caption]
Lo formidable del mundo cuántico es que la restricción Newtoniana para la combinación de energías no es válida cuando se trata de partículas como los electrones o los fotones. Los sistemas cuánticos pueden existir en regiones que son prohibidas clásicamente, lo que les permite atravesarlas por completo para romper el confinamiento clásico. En el ejemplo de la barrera de potencial, es como si les fuera permitido adquirir energía cinética negativa para continuar su movimiento de izquierda a derecha, más allá de la barrera. (Figura 1). Esta propiedad conocida como efecto túnel, es exclusiva de los sistemas cuánticos.
El primer estudio del efecto túnel se realizó en 1927, justo cuando Heisenberg publicaba sus resultados sobre el principio de incertidumbre, que marcarían la culminación de la estructura formal de la teoría cuántica. Friedrich Hund (1896-1997) publica una serie de trabajos en Zeitschrift für Physik [3] donde resuelve por primera vez la entonces nueva ecuación de Schrödinger para un potencial de pozo doble. El objetivo era modelar las interacciones de los átomos en la conformación de moléculas. Tratándose de un pozo doble, el potencial es una función que tiene dos mínimos locales (los pozos) y un máximo local (barrera de potencial entre los pozos), y que diverge asintóticamente hacia ambos extremos de la recta. Como buen físico moderno, Hund buscaba estados simétricos y anti-simétricos que contribuyeran a la energía de amarre de los átomos en las moléculas. Sus resultados muestran que el efecto túnel es indispensable para la estabilidad molecular, permitiendo que los átomos se agrupen simétrica o anti-simétricamente en los pozos.
Casi al mismo tiempo, también en 1927, Lothar Nordheim (1899-1985) estudia la transición de un estado confinado a un estado libre por medio del efecto túnel a través de una barrera cuadrada [4]. Después, en colaboración con Ralph Fowler (1889-1944), se perfeccionó el modelo de tal forma que pudieron describir la emisión termiónica de electrones por metales en presencia de campos eléctricos muy intensos [5]. El campo eléctrico modifica la forma cuadrada de la barrera de potencial y lo lleva a una forma triangular, que ellos resolvieron usando teoría WKB. Este tipo de efecto túnel se conoce como tunelamiento Fowler-Nordhein. En ambos casos, barreras cuadrada y triangular, a los estados energéticos que permiten que la partícula abandone el confinamiento clásico para moverse libremente más allá de la barrera, se les conoce hoy en día como estados metaestables o estados de Gamow.
En 1928 George Gamow aplica el efecto túnel para modelar la desintegración que se observa en algunos núcleos atómicos pesados [6]. La suma de interacciones nucleares crea una barrera de potencial que retiene confinados a los nucleones. El trabajo de Gamow muestra que, eventualmente, una pequeña porción de nucleones logra atravesar la barrera de confinamiento y abandona al núcleo. El remanente nuclear corresponde a otro elemento atómico, proceso que se conoce como decaimiento alfa. Sin el efecto túnel, este tipo de desintegración nuclear no podría existir. Las partículas alfa, emitidas durante el decaimiento, son núcleos de helio compuestos por dos protones y dos neutrones. De acuerdo con Gamow, estas partículas satisfacen una condición energética muy especial, pues requieren de energías complejas conocidas como resonancias, cuya parte real corresponde a la energía de confinamiento clásico y el inverso de su parte imaginaria concierne al tiempo de vida media, es decir, al promedio estadístico del tiempo que tarda la partícula alfa en escapar del núcleo. Si bien estas energías complejas resultan extrañas incluso para la mecánica cuántica, sus partes real e imaginaria son cantidades que pueden medirse en el laboratorio. Por ello, a esta clase de estados se les conoce como metaestables.
El primer ejemplo del efecto túnel realizado por átomos completos al atravesar una barrera de potencial fue desarrollado por Dennison y Uhlenbeck en 1932 [7]. Los átomos de hidrógeno en la molécula de amoniaco (NH3) definen un plano que implica confinamiento clásico para el átomo de nitrógeno. Los tres hidrógenos, como un todo, interactúan con el nitrógeno por medio de una barrera de potencial definida entre ellos, a lo largo de dicho plano. La molécula de amoniaco (NH3) presenta un proceso de inversión cuando el átomo de nitrógeno rompe el confinamiento y pasa de un lado al otro de la barrera por medio del efecto túnel. Si bien este fenómeno de inversión es sorprendente porque es un átomo completo, no solo un electrón o una porción de núcleo, el que tunelea una barrera de potencial, sigue tratándose de un solo sistema cuántico, cuyas dimensiones escapan a nuestros sentidos.
A estas alturas cabe preguntarse si acaso el efecto túnel puede presentarse para más de un sistema cuántico a la vez, o para algún sistema cuyas dimensiones superen las características atómicas. Por ejemplo, en 2002, con miras únicamente didácticas, Olaf Nairz, Markus Arndt y Anton Zeilinger (Premio Nobel de Física 2022), demostraron experimentalmente que moléculas tan grandes como los fulerenos C60, que se comportan como partículas macroscópicas en circunstancias ordinarias, exhiben interferencia cuántica cuando se les somete al experimento de doble rendija [8]. Si un objeto “tan grande” como el C60 comparte propiedades de interferencia con elementos “tan pequeños” como los electrones o los fotones, ¿por qué no investigar la posibilidad de encontrar un efecto túnel macroscópico?
Justo en este año de festejos cuánticos, en su anuncio del 7 de octubre, la Real Academia Sueca de Ciencias informó que los distinguidos con el Premio Nobel de Física 2025 son, de forma conjunta, John Clarke, Michael H. Devoret y John M. Martinis “por el descubrimiento del efecto túnel macroscópico de la Mecánica Cuántica y la cuantización de la energía en un circuito eléctrico” [9].
Para entender las aportaciones realizadas por estos tres investigadores se requiere de otros conceptos básicos. Los cuerpos sólidos se pueden modelar como un arreglo ordenado de átomos y un enjambre de electrones, que está sujeto a las interacciones promedio de la red atómica, por lo que algunos de ellos terminan débilmente amarrados a su respectivo átomo. La energía de amarre puede romperse por medio de un voltaje aplicado a la red, lo que genera una corriente eléctrica que fluye a lo largo de la red. A mayor energía de amarre, los electrones ofrecen mayor resistencia a incorporarse a la corriente eléctrica -la ley de Ohm indica que la corriente es proporcional al voltaje e inversamente proporcional a la resistencia-. Hay materiales que ofrecen mayor energía de amarre, por lo que los electrones presentan mayor resistencia que otros. El cobre es uno de los materiales que ofrece poca resistencia, por lo que es un buen conductor de corriente eléctrica. Materiales como la madera seca, el plástico o la porcelana ofrecen mucha resistencia, por lo que son aislantes, esto es, malos conductores de corriente eléctrica.
Este comportamiento de la materia resulta accesible a nuestros sentidos, por lo que su clasificación en conductores y aislantes parece casi natural. En 1911 Kamerlingh Onnes encontró que la resistencia del mercurio solido disminuye abruptamente cuando se le enfría por debajo de -269 grados Celcius. El descubrimiento de este fenómeno, nombrado superconductividad por el mismo Onnes, le mereció el Premio Nobel de Física en 1913. Toda vez que no estamos habituados a vivir en temperaturas tan extremas, la experiencia cotidiana nuevamente falla: no cabría esperar que disminuyendo la temperatura se consigue disminuir la resistencia en un material.
Hoy en día entendemos que la condición de ser aislante, conductor o superconductor obedece a diferentes fases de la materia que dependen del comportamiento colectivo de los electrones que la conforman. Los electrones tienen personalidades múltiples que pueden caracterizarse por su energía o por su espín -este último se comporta como una brújula diminuta en presencia de un campo magnético, alineándose paralela o anti paralelamente a éste-. Además, como se ha indicado, son Fermiones. Cada uno de los electrones del enjambre ocupa el estado energético mas bajo que le es posible, por lo que esos estados se van saturando poco a poco hasta alcanzar un nivel energético por debajo de la Energía de Fermi, que determina el umbral de la energía de amarre promedio en la red atómica. Cuando se aplica un voltaje, los electrones se excitan y alcanzan los estados energéticos que queden libres. Dependiendo del material, la densidad de electrones puede o no superar los sitios a ocupar en los niveles energéticos. En el primer caso, conductores, algunos electrones alcanzan energías superiores a la de Fermi y circulan libremente a lo largo de la red atómica. En el segundo caso, aislantes, a pesar de existir sitios libres en los estados energéticos superiores, los electrones no pueden escalarlos para superar la energía de Fermi porque su naturaleza Fermiónica se los impide.
En los superconductores ocurre un fenómeno por demás interesante: los electrones se entrelazan en pares, sus estados se correlacionan, por lo que no se les puede describir de forma independiente. El comportamiento del par, como un todo, deja de obedecer la estadística de Fermi-Dirac y se comporta como un bosón. Así que estos pares pueden aglomerarse, agrupándose en el mismo estado y compartiendo la misma energía, la más baja posible. Este fenómeno es conocido como condensación de Bose-Einstein. Cuando se aplica un voltaje, los pares electrónicos transitan a un estado de energía más alto y producen una corriente eléctrica. El marco teórico asociado con el comportamiento de los pares electrónicos, actualmente llamados pares de Cooper, fue desarrollado por John Bardeen, Leon Cooper y John Robert Schrieffer, por lo que se hicieron merecedores al Premio Nobel de Física en 1972.
El premio de este año reconoce experimentos que muestran la forma en la que el efecto túnel puede observarse a escala macroscópica. Si dos superconductores se unen junto con una barrera delgada de aislante, entre ellos se crea una unión de Josephson. A mediados de los años ochenta, John Clarke, Michel Devoret y John Martinis mostraron que podían controlar el perfil bosónico de los pares de Cooper para romper el confinamiento clásico definido por el aislante de la unión de Josephson, consiguiendo el efecto túnel para un par de electrones a la vez. Los laureados también fueron capaces de mostrar que el sistema está cuantizado, lo que significa que solo absorbe o emite energía en cantidades específicas (fotones). Dado que los pares de Cooper están correlacionados, resultan de utilidad para codificar información en forma cuántica (qubits), por lo que las aplicaciones del efecto túnel macroscópico se extienden a las tecnologías cuánticas que están, como sabemos, en pleno desarrollo.
Referencias
[1] O. Rosas-Ortiz, El Premio Nobel de Física 2022, Avance y Perspectiva, Vol 8, Núm 3, octubre 15 de 2022 (https://avanceyperspectiva.cinvestav.mx/premio-nobel-de-fisica-2022/)
[2] Nobel Prize in Physics 1973
(https://www.nobelprize.org/prizes/physics/1973/summary), visitado el 18 de octubre de 2025
[3] F. Hund, Zur Deutung der Molekelspektren. I, Z. Phys. 40, 742-764 (1927)
(https://link.springer.com/article/10.1007/BF01400234); F. Hund, Zur Deutung der Molekelspektren. II, Z. Phys. 42, 93-120 (1927)
(https://link.springer.com/article/10.1007/BF01397124); F. Hund, Zur Deutung der Molekelspektren. III, Z. Phys. 42, 805-826 (1927)
(https://link.springer.com/article/10.1007/BF01397249)
[4] L. Nordheim, Zur Theorie der thermischen Emission und der Reflexion von Elektronen an Metallen, Z. Phys. 46, 833-855 (1928)
(https://link.springer.com/article/10.1007/BF01391020); L. Nordheim, Zur Quantentheorie des Atomkernes, Z. Phys. 51, 204-212 (1928)
(https://link.springer.com/article/10.1007/BF01343196)
[5] R.H. Fowler and L. Nordheim, Electron emission in intense electric fields, Proc. R. Soc. London, Ser. A 119, 173 (1928)
(https://royalsocietypublishing.org/doi/10.1098/rspa.1928.0091)
[6] G. Gamow, Zur Quantentheorie des Atomkernes, Z. Phys. 51, 204-212 (1928)
(https://link.springer.com/article/10.1007/BF01343196)
[7] D.M. Dennison and G.E. Uhlenbeck, The Two-Minima Problem and the Ammonia Molecule, Phys. Rev. 41, 313–321 (1932)
(https://journals.aps.org/pr/abstract/10.1103/PhysRev.41.313)
[8] O. Nairz, M. Arndt and A. Zeilinger, Quantum interference experiments with large molecules, Am. J. Phys. 71, 319-325 (2002)
(https://pubs.aip.org/aapt/ajp/article-abstract/71/4/319/1042923/Quantum-interference-experiments-with-large?redirectedFrom=fulltext)
[9] Nobel Prize in Physics 2025
(https://www.nobelprize.org/prizes/physics/2025/summary/), visitado el 18 de octubre de 2025
*Foto de portada: Niklas Elmehed © Nobel Prize Outreach
Oscar Rosas-Ortiz
Profesor Investigador del Departamento de Física. Miembro del Sistema Nacional de Investigadoras e Investigadores, Nivel III. Miembro de la Academia Mexicana de Ciencias.